Question

What is the S12 of the geometric sequence? Round to the nearest whole number.

Answer 1

We were given the geometric sequence 16, 24, 36, 54 and we are told to find

`S_(12)`

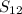
This means to find the sum of the first 12 terms.

From the sequence

`\begin{gathered} \text{the first term a = 16} \\ \text{the common ratio r = }(24)/(16)=(3)/(2) \\ n\text{umber of terms n = 12} \end{gathered}`

Sum of a geometric sequence is given as

`\begin{gathered} S_n=(a(r^n-1))/(r-1) \\ \text{since r }>\text{ 1} \end{gathered}`

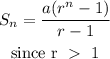
So, we have

`\begin{gathered} S_n=(a(r^n-1))/(r-1) \\ S_(12)=(16(((3)/(2))^(12)-1))/((3)/(2)-1) \\ S_(12)=(16(128.7464))/(0.5) \\ S_(12)=4119.8848 \end{gathered}`

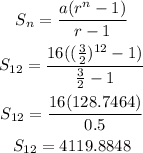
Hence to the nearest whole number, the answer is 4,120 second option