To solve this problem, first, let's find the speed of the father.
Let x be the speed of the father.
The speed is distance/time.
Then,

Second, let's find the speed of the soon.
Let y represent the speed of the soon.
Since the speed is twice the speed of the father:
y = 2x:
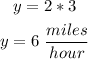
Finally, find the distance traveled in 9 hours.
The distance is the product of the time and the speed:
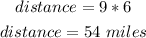
Answer: 54 miles.