Question

Hi, can you help me answer this question please, thank you

Answer 1

Write out the given parameters in the questions

`\begin{gathered} \text{standard deviation =0.4 } \\ \text{sample ,n=20} \end{gathered}`

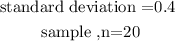
The critical value is the measurement used to calculate the margin of error within a set of data and is expressed as

`\begin{gathered} \text{Critical value =}1-(\alpha)/(2) \\ \text{where } \\ \alpha=0.05 \end{gathered}`

Then

`\text{critical value is the z=1.960}`

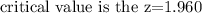
Therefore the critical value is1.960

Then the standard error is given by

`\begin{gathered} \sigma_{\bar{x}}=\frac{\sigma}{\sqrt[]{n}} \\ \\ \text{where } \\ n=\text{sample space=20 and }\sigma=0.4 \end{gathered}`

Substituting the value we have

`\sigma_{\bar{x}}=\frac{0.4}{\sqrt[]{20}}=(0.4)/(4.47)=0.089`

Therefore the standard error is 0.089

The confidence interval is given by

`\begin{gathered} \text{Confidence interval=}\bar{x}\pm(1.96)(S.E) \\ \text{where S.E= standard error } \end{gathered}`

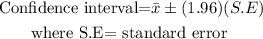
The mean for the sample will be

`\bar{x}=\frac{sum\text{ of data}}{n}=(3497.76)/(20)=173.988`

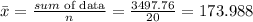
Substitute the value to obtain the confidence interval

`\begin{gathered} \text{confidence interval=173.988}\pm1.96*0.089 \\ C.I=173.988\pm0.174 \\ C\mathrm{}I=(173.814,174.162) \end{gathered}`

Therefore, the confidence interval is (173.81,174.16) to 2d.p