Question

The length of the longer leg of a right triangle Is 16 cm more than four times the length of the shorter leg. The length of the hypotenuse is 17 cm more thanfour times the length of the shorter leg. Find the side lengths of the triangle.Length of the shorter leg:amLength of the longer leg:cmLength of the hypotenuse:17 cm

Answer 1

The Solution.

Representing the given information in a diagram.

Applying Pythagorean Theorem on the right-angled triangle above, we get

`\begin{gathered} (4x+17)^2=x^2+(4x+16)^2 \\ C\text{learing the brackets, we get} \\ 4x(4x+17)+17(4x+17)=x^2+4x(4x+16)+16(4x+16) \end{gathered}`
`16x^2+68x+68x+289=x^2+16x^2+64x+64x+256`

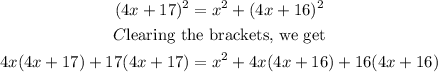
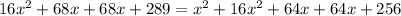
Collecting the like terms, we get

`16x^2-16x^2-x^2+136x-128x+289-256=0`
`\begin{gathered} -x^2+8x+33=0 \\ \text{Multiplying through by -1, we get} \\ x^2-8x-33=0 \end{gathered}`

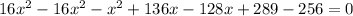
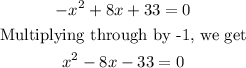
Solving quadratically by factorization method, we get

`\begin{gathered} x^2+3x-11x-33=0 \\ (\text{Having substituted +3x and -11x for -8x)} \end{gathered}`
`\begin{gathered} x(x+3)-11(x+3)=0 \\ (x+3)(x-11)=0 \end{gathered}`
`\begin{gathered} x+3=0\text{ or x-11=0} \\ x=-3\text{ or x = 11} \end{gathered}`

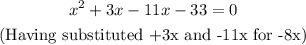
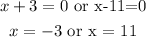
Since the length of a side of a triangle cannot be negative, we discard x = -3.

So, the correct length for the shortest side of the triangle is 11cm

The longer side = 4x+16 = 4(11)+16 = 44+16 = 60cm

The hypotenuse side = 4x+17 = 4(11) +17 = 44+17 =61cm.

Therefore, the correct answer is

11cm, 60cm, and 61cm