Question

ActivityIn this activity, you will transform an equation in a system of linear equations by multiplying both sides of the equation by a constant. Then youwill then eliminate one variable by adding the modified equation to the other original equation to find the solution for the variable that is noteliminated.A carnival charges $3 for kids and $10 for adults. On Saturday, there were 500 visitors, and the total amount taken at the gate was $3,600. Theequation representing the number of visitors is k + a = 500, where k represents the number kids and a represents the number of adults. Theequation representing the amount of money collected is 3k + 100 = 3,600. How many kids and adults visited the carnival?Part ABefore solving this problem, decide which tool you'll use to solve it. Which method for solving systems of linear equations is best for solving thisproblem? Explain your answer.

Answer 1

The system of equations we have is

`\begin{gathered} k+a=500 \\ 3k+10a=3600 \end{gathered}`

We first multiply the top equation by 3 to get

`3k+3a=1500`

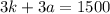
and therefore, our system becomes

`\begin{gathered} 3k+3a=1500 \\ 3k+10a=3600 \end{gathered}`

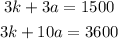
subtracting the top equation from the bottom equation gives

`7a=3600-1500`
`7a=2100`

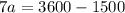
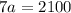
finally, dividing both sides by 7 gives

`a=(2100)/(7)`
`a=300`

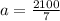
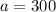
with the value of a in hand, we now find the value of k

`\begin{gathered} k+a=500 \\ k+300=500 \end{gathered}`

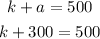
subtracting 300 from both sides gives

`\begin{gathered} k=500-300 \\ k=200 \end{gathered}`

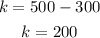
Hence, the solution to the system is a = 300 and k = 200, meaning 300 adults and 200 kids visited the carnival.