Hello there. To solve this question, we'll need to remember some properties about trigonometry.
Let's start by drawing the situation:
Since we don't know Jane's height, we don't need to consider the point of view starting by her eye height. In this case, we can solve directly for the height of the monument.
For this, we'll use the tangent. This trigonometric function relates the opposite side to an angle to its adjacent side by the following ratio:
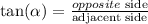
Using opposite side as h (for height), adjacent side is the distance between Jane and the monument, 1000 and alpha equals to the angle 29º, we have:
tan(29º) = h/1000
Multiply both sides of the equation by 1000
h = 1000tan(29º)
Using a calculator, we have that tan(29º) is approximately equal to 0.5543
Hence, we have that
h approx. 55.43 meters.