The method of elimination consists in changing one of the equations in such a way that when both are summed we can eliminate one variable. This change is usually done by multiplying one or more constants to the equation we want to change. In this case if we multiply either equation by "-1" we will have the variable "y" with oposite signs and same absolute value, this would indicate that if we sum both equations the variable will be eliminated. Let's try it out:
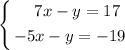
Multiplying the first one by "-1".
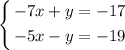
Now the "y" variable has oposite signs and we can add the equations.
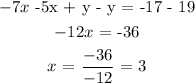
We can now use either equation to find the value of "y" by using the value of "x" we calculated.
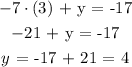
The solution to the system is x = 3 and y = 4. Which would be the last option.