Question

The population of mice doubles every year. There are 10 mice in the population. Write an exponential function to model this situation:Determine the population of the mice in 11 years. How many years will it take for the population of mice to reach at least 10 million?

Answer 1

Let's list down the given information in the problem.

1. initial value = 10 mice

2. rate = doubles every year = 200%

3. time = 11 years

4. final value = at least `10 million

The equation of an exponential function goes by this pattern:

`f(x)=ab^x`

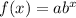
where a = initial value, b = growth rate, x = time in years

From the given information, we can write an exponential model of the situation by plugging in those given data (1 and 2 only) to the pattern above.

`f(x)=10(2)^x`

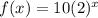
The exponential model is f(x) = 10(2)^x as shown above.

After 11 years, the population will be: (plug in x = 11 to the model)

`\begin{gathered} f(x)=10(2)^(11) \\ f(x)=10(2048) \\ f(x)=20,480 \end{gathered}`

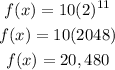
After 11 years, the population of the mice will have been 20, 480.

To calculate how many years it will take the population to reach at least 10 million, we will have to assume that f(x) = 10 million and solve for x.

`10,000,000=10(2)^x`
`\begin{gathered} \text{Divide both sides by 10.} \\ 1,000,000=2^x \\ Convert\text{ to logarithmic form.} \\ \log _21,000,000=x \\ x\approx19.93 \\ x\approx20 \end{gathered}`

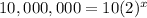
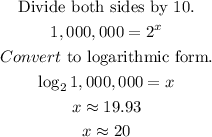
Thus, it will take approximately 20 years for the population of the mice to at least reach 10 million.