Rewrite the ratios in such a way that the number that corresponds to b is the same in both.
Since a:b = 2:5 and b:c = 3:4, then, the numbers that correspond to b are 5 and 3.
The least common multiple of 3 and 5 is 15. Multiply the first ratio by 3 and the second ratio by 5 in order to get two ratios with the same number for b:
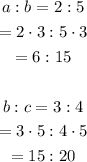
Since a:b = 6:15 and b:c = 15:20, then:
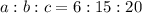
Therefore, the answer is: a:b:c = 6:15:20.