Question

The total amount of money in an account with P dollars invested in it is given by the formulaA = P + Prt.where r is the rate expressed as a decimal and t is time (in years).If $1862 is invested at 5 %, how much money will be in the account after 6 months? Round your answer to the nearest cent.

Answer 1

The amount in the account after 6 months is 1908.55

Using the formula given ;

• A = P + Prt
• P = principal = 1862
• r = rate = 5% = 0.05
• time = 6 months = 1/2 = 0.5 years

Inputting the values into the formula ;

A = 1862 + (1862 × 0.05 × 0.5)

A = 1862 + 46.55

A = 1908.55

The amount in the account after 6 months is 1908.55

Answer 2

Given the formula:

`A=P+Prt`

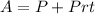
You know that "A" is the amount, "P" is the number of dollars invested" r" is the rate (as a decimal), and "t" is time in years.

In this case, you can identify that:

`\begin{gathered} P=1862 \\ \\ r=(5)/(100)=0.05 \end{gathered}`

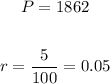
Remember that a percent can be converted to a Decimal Number by dividing it by 100.

Knowing that 1 year has 12 months, you can determine that 6 months is a half of a year:

`t=(1)/(2)`

Then, substituting values into the formula and evaluating, you get:

`\begin{gathered} A=P+Prt \\ A=1862+(1862)(0.05)((1)/(2)) \end{gathered}`
`\begin{gathered} A=1862+46.55 \\ A=1908.55 \end{gathered}`

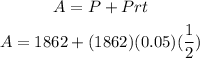
Therefore, the answer is: $1908.55