The hourly wage after t years is given by the expression:
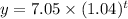
In this case, we need to find the amount of time after which he will be earning $10.00 per hour, then we have to solve for t from the above equation, like this:
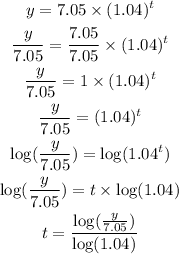
Then, we just have to replace $10.00 for y into the above expression and then calculate the value of t, like this:
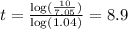
Then, the