ANSWER
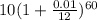
Step-by-step explanation
We want to find the expression that represents the number of books after 5 years.
To do this, we have to apply the general formula for the amount of an exponential increase based on a 12 month time period:

where P = initial amount
r = rate
x = amount of time (number of years)
From the question:
P = 10,000
r = 1% = 0.01
t = 5 years
Therefore, the expression that represents the number of books (in thousaands) after 5 years is:

That is the answer.