Question

Mr. Gordon’s science class is studying blood types. The table below shows the probability that a person living in the US has a particular blood type. The probability of having a blood type: O= 9/20; A= 41/100; B= 1/10; and AB= 1/25What is the probability that three students selected randomly from the class will have A, B, and AB blood, respectively?A.) 41/25,000 or 0.16%B.) 41/2500 or 1.64%C.) 43/25,000 or 0.17%D.) 43/135 or 31.9%

Answer 1

Given the probability of having a blood type:

O = 9/20

A = 41/100

B = 1/10

AB = 1/25

Let's find the probability that three students selected at random from the class will have A, B, and AB blood respectively.

Let's first verify if the events are mutually dependent or independent:

`\begin{gathered} (9)/(20)+(41)/(100)+(1)/(10)+(1)/(25) \\ \\ (5(9)+1(41)+10(1)+4(1))/(100) \\ \\ (45+41+10+4)/(100) \\ \\ =(100)/(100) \\ \\ =1 \end{gathered}`

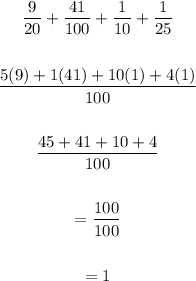
Since the total probability is 1, the events are mutually independent.

Since the events are mutually independent, to find the probability a randomly selected student will have A, B, and AB blood respectivel, we have:

`\begin{gathered} P(A)*P(B)*P(AB) \\ \\ =(41)/(100)*(1)/(10)*(1)/(25) \\ \\ =(41*1*1)/(100*10*25) \\ \\ =(41)/(25000) \\ \\ =0.00164\approx0.16\text{ \%} \end{gathered}`

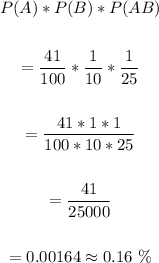
Therefore, the probability that three students selected randomly from the class will have A, B, and AB respectively is 41/25,000 or 0.16%

ANSWER:

A.) 41/25,000 or 0.16%