Question

The formula gives the volume V of a right cylinder with radius r and height h.V = πr²hSolve for r

Answer 1

The formula that gives the volume V of a right cylinder with radius r and height h is presented below:

`V=\pi r^2h`

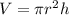
Step 1: Divide both sides by πh

`\begin{gathered} (V)/(\pi h)=(\pi r^2h)/(\pi h) \\ r^2=(V)/(\pi h) \end{gathered}`

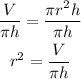
Step 2: Take the square root of both sides.

`\begin{gathered} \sqrt[]{r^2}=\sqrt[]{(V)/(\pi h)} \\ r=\sqrt[]{(V)/(\pi h)} \end{gathered}`

Step 3: We can multiply both the numerator and denominator by πh to get:

`\begin{gathered} r=\sqrt[]{(V\pi h)/(\pi^2h^2)} \\ =\frac{\sqrt[]{V\pi h}}{\sqrt[]{\pi^2h^2}} \\ r=\frac{\sqrt[]{V\pi h}}{\pi h} \end{gathered}`

The correct option is the last one.