The notation f(-3) indicates that you have to calculate the value of the function f(x) for x=3.
To determine which value has the largest value for f(-3) you have to replace each function with x=3 and calculate the corresponding value of f(x)
1.
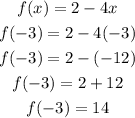
2.
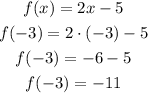
3.
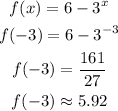
4.
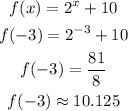
Now that we calculated f(-3) for each one of the functions, you can compare them.
The function that has the largest value of f(-3) is the first one: f(x)=2-4x