1 Answer

Alexander Terekhov · Answer 1 · 2023-04-26T20:16:34+0000

in the given triangle,

AB = BC = 6

As, the two sides are equal so, the given triangle is isosceles.

also, the angle < ABC = 120 degrees,

the area of the isosceles triangle is,

$A=(1)/(2)* a^2*\sin \theta^{}$

here a = length of two congruent sides,

theta = the angle between congruent sides.

put the values,

A = 1/2 x 6^2 x sin 120

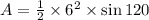
$A=(1)/(2)*6^2*\sin 120$
$\begin{gathered} A=(36)/(2)*\frac{\sqrt[]{3}}{2} \\ A=9\sqrt[]{3} \end{gathered}$

thus, the correct answer is option D

Please log in or register to add a comment.