Answer:
(a) The volume of water is 100 cm³
(b) The volume of the rock is 20 cm³
(c) The density of the rock is 30 g/cm³
Step-by-step explanation:
The given parameters of the perspex box are;
The area of the base of the box, A = 10 cm²
The initial level of water in the box, h₁ = 10 cm
The mass of the rock placed in the box, m = 600 g
The final level of water in the box, h₂ = 12 cm
(a) The volume of water in the box, 'V', is given as follows;
V = A × h₁
∴ The volume of water in the box, V = 10 cm² × 10 cm = 100 cm³
The volume of water in the box, V = 100 cm³
(b) When the rock is placed in the box the total volume,
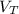 , is given by the sum of the rock,
, is given by the sum of the rock,
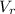 , and the water, V, is given as follows;
, and the water, V, is given as follows;
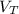 =
=
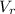 + V
+ V
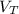 = A × h₂
= A × h₂
∴
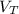 = 10 cm² × 12 cm = 120 cm³
= 10 cm² × 12 cm = 120 cm³
The total volume,
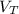 = 120 cm³
= 120 cm³
The volume of the rock,
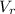 =
=
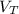 - V
- V
∴
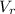 = 120 cm³ - 100 cm³ = 20 cm³
= 120 cm³ - 100 cm³ = 20 cm³
The volume of the rock,
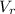 = 20 cm³
= 20 cm³
(c) The density of the rock, ρ = (Mass of the rock, m)/(The volume of the rock)
∴ The density of the rock, ρ = 600 g/(20 cm³) = 30 g/cm³