Question

A colony of 32 bacteria doubles in every 4 hours. How many bacteria are in the colony after 16 hours?

Answer 1

Answer:

The number of bacteria in the colony after 16 hours = 992

Step-by-step explanation:

The bacteria doubles every 4 hours and we are considering 16 hours

The number of times that the bacteria doubles is 16/4 = 4 times

Note that there is a first term and four other terms when the bacteria were doubled

There are 5 terms in total

Number of terms, n = 5

The initial amount of bacteria, a = 32

The bacteria doubles every 4 hours

That is, the common ratio, r = 2

Since there is a common ratio, this is a geometric progression.

The sum of n terms of a geometric progression is given as:

`S_n=(a(r^n-1))/(r-1)`

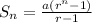
Substitute a = 32, r = 2, and n = 5 into the formula above to get the number of bacteria in the colony after 16 hours

`\begin{gathered} S_4=(32(2^5-1))/(2-1) \\ S_4=(32(32-1))/(1) \\ S_4=32(31) \\ S_4=992 \end{gathered}`

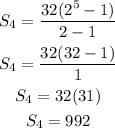
The number of bacteria = 992