Question

An automobile engine can run on a mixture of gasoline and a substitute fuel. If gas costs $3.25 per gallon and the substitute fuel costs $2 per gallon, what percent of a mixture must be substitute fuel to bring the cost down to $2.25 per gallon?

Answer 1

80%

Step-by-step explanation

To make a gallon costing $2.25, let x amount of gas mix with y amount of substitute fuel,

`\begin{gathered} y\text{ + x = 1} \\ y\text{ = 1-x ..............equ 1} \end{gathered}`
`3.25\text{ x + 2y = 2.25 ............................equ 2}`

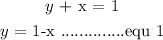
Substitute equation 1 into 2

`\begin{gathered} 3.25x\text{ + 2\lparen1 - x\rparen = 2.25} \\ 3.25x\text{ + 2 - 2x = 2.25} \\ 1.25x\text{ = 0.25} \\ x\text{ = }(0.25)/(1.25) \\ x\text{ = 0.2} \end{gathered}`

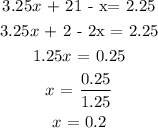
Determine the percent of substitute fuel

From equation 1:

y = 1 - x

y = 1 - 0.2

y = 0.8 = 80%.

Hence, 80 percent of the mixture must be substitute fuel to bring the cost down to $2.25 per gallon.