ANSWER
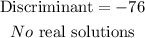
Step-by-step explanation
We want to find the discrimininant of the equation:
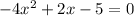
The general form of a quadratic equaion is given as:

The discriminant is given as:
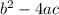
Therefore, we need to find that.
From the given equation:
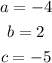
Therefore, we have that the discriminant is:
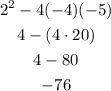
That is the discriminant.
Since the discriminant is less than 0, then there are no real solutions of the equation.