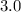Question

1. What is the standard deviation of the data {7, 1, 7, 10, 5, 3, 2}?to the nearest whole numberOPTIONS3.0, 2.7, 5.0, and 9.0

Answer 1

Answer: 3.0

Step-by-step explanation:

Answer 2

Step-by-step explanation:

The set of numbers are given below as

`7,1,7,10,5,3,2`

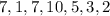
Concept:

The formula for standard deviation is given below as

`\begin{gathered} \sigma\left(X\right)=\sqrt{\frac{\sum_(i=1)^7\left(x_i-\bar{x}\right)^2}{n-1}} \\ where, \\ \bar{x}=mean \\ n=7 \end{gathered}`

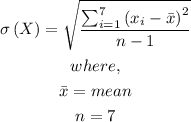
Step 1:

We will calculate the mean of the set of data

`\begin{gathered} \bar{x}=(sumofnumbers)/(numberofdata)=(7+1+7+10+5+3+2)/(7) \\ \bar{x}=(35)/(7)=5 \end{gathered}`

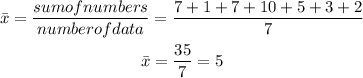
Step 2:

Calculate the mean deviation below

`x-\bar{x}`
`\begin{gathered} 7-5=2 \\ 1-5=-4 \\ 7-5=2 \\ 10-5=5 \\ 5-5=0 \\ 3-5=-2 \\ 2-5=-3 \end{gathered}`

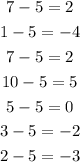
Step 3:

Calculate the squares of the mean deviation

`(x-\bar{x})^2`
`\begin{gathered} 2^2=4 \\ (-4)^2=16 \\ 2^2=4 \\ 5^2=25 \\ 0^2=0 \\ (-2)^2=4 \\ (-3)^2=9 \end{gathered}`

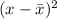
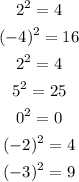
Step 4:

Substitute the values in the formula below

`\begin{gathered} \sigma \left(X\right)=\sqrt{\frac{\sum _(i=1)^n\left(x_i-\bar{x}\right)^2}{n-1}} \\ \sigma\left(X\right)=\sqrt{(4+16+4+25+0+4+9)/(7-1)} \\ \sigma\left(X\right)=\sqrt{(62)/(6)} \\ \sigma\left(X\right)=3.21 \end{gathered}`

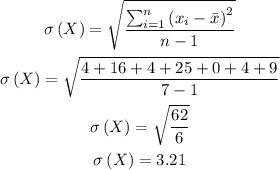
Hence,

The standard deviation of the data to the nearest whole number will be

`3.0`