Solution:
Given the equations:
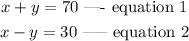
To solve for an expression equal to y, using the first equation, we make y the subject of the formula in equation 1.
Thus, from equation 1,
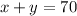
Add -x to both sides of the equation.
Thus,
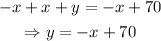
Hence, we have
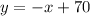
The third option is the correct answer.