We want to find the intervals of concavity of the function;
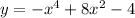
We start by taking the second derivatives;
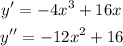
When a function is concave up, the second derivative is positive, thus; we seek the intervals where;
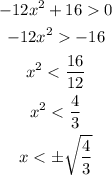
Let's find the points of inflection, this is where the second derivative is zero;
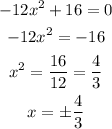
The y values will be;
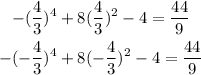
Thus, the answers are;
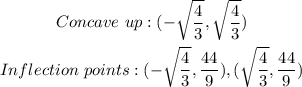
Thus the answer is option D;
This is a sign chart for the second derivative;