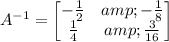Question

Answer answer your answer by filling in the blank boxes

Answer 1

We are given the following 2x2 matrix

`A=\begin{bmatrix}{-3} & {-2} \\ {4} & {8}\end{bmatrix}`

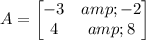
We are asked to find the inverse of matrix A.

Recall that the inverse of a 2x2 matrix is given by

`A^(-1)=(1)/(ad-bc)*\begin{bmatrix}{d} & {-b} \\ {-c} & {a}\end{bmatrix}`

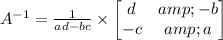
Where

a = -3

b = -2

c = 4

d = 8

Let us substitute these values into the above equation

`A^(-1)=(1)/((-3)(8)-(-2)(4))*\begin{bmatrix}{8} & {-(-2)} \\ {-(4)} & {-3}\end{bmatrix}`

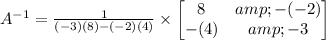
Now simplify

`\begin{gathered} A^(-1)=(1)/(-24+8)*\begin{bmatrix}{8} & {2} \\ {-4} & {-3}\end{bmatrix} \\ A^(-1)=(1)/(-16)*\begin{bmatrix}{8} & {2} \\ {-4} & {-3}\end{bmatrix} \\ A^(-1)=\begin{bmatrix}{(8)/(-16)} & {(2)/(-16)} \\ {(-4)/(-16)} & {(-3)/(-16)}\end{bmatrix} \\ A^(-1)=\begin{bmatrix}{-(1)/(2)} & {-(1)/(8)} \\ {(1)/(4)} & {(3)/(16)}\end{bmatrix} \end{gathered}`

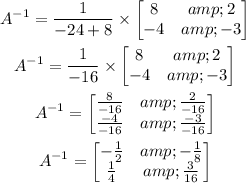
Therefore, the inverse of the matrix A is

`A^(-1)=\begin{bmatrix}{-(1)/(2)} & {-(1)/(8)} \\ {(1)/(4)} & {(3)/(16)}\end{bmatrix}`