1 Answer

Ask a Question

Derrick Zhang · Answer 1 · 2023-09-27T10:04:09+0000

ANSWER

The slope of the equation of the line is y =x - 2

Explanation:

What to find? The equation that passes through the lines given

Given parameters

Line A = (-1, -3)

Line B = (1, -1)

The first thing is to find the slope

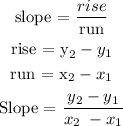
$\begin{gathered} \text{slope = }\frac{rise}{\text{run}} \\ \text{rise = y}_2-y_1 \\ \text{run = x}_2-x_1 \\ \text{Slope = }\frac{y_2-y_1}{x_{2\text{ }}-x_1} \end{gathered}$

According to the point given

let

x1 = -1

y1 = -3

x2 = 1

y2 = -1

Substitute the above data into the slope formula

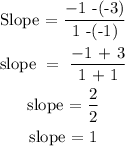
$\begin{gathered} \text{Slope = }\frac{-1\text{ -(-3)}}{1\text{ -(-1)}} \\ \text{slope }=\text{ }\frac{-1\text{ + 3}}{1\text{ + 1}} \\ \text{slope = }(2)/(2) \\ \text{slope = 1} \end{gathered}$

The slope of the two lines in 1

Recall that, the slope-intercept equation of a line is given as

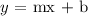
$y\text{ = mx + b}$

Where

m = slope of the line

b = intercept of the y-axis

$\begin{gathered} (y\text{ - y1) = m(x - x1)} \\ m\text{ = 1} \\ \lbrack(y\text{ - (-3)\rbrack= 1\lbrack(x - (-1)\rbrack} \\ \text{open the parentheses} \\ y\text{ + 3 = 1(x + 1)} \\ y\text{ + 3 = x + 1} \\ \text{Substract 3 from both sides} \\ y\text{ + 3 - 3 = x + 1 - 3} \\ y\text{ = x + 1 -}3 \\ y\text{ = x - 2} \end{gathered}$

Hence, the equation that passes through the line is y = x - 2

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions