The Pythagorean Theorem states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares of the other two sides in a right triangle.
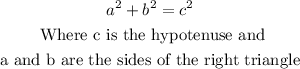
Graphically
So, in this case, you have
![\begin{gathered} a^2=225in^2 \\ b^2=64in^2 \\ a^2+b^2=c^2 \\ 225in^2+64in^2=c^2 \\ 289in^2=c^2 \\ \text{ Apply square root to both sides of the equation} \\ \sqrt[]{289in^2}=\sqrt[]{c^2} \\ 17in=c \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/osf3duxvkvkl9r8rx00w1etrq1595od3e9.png)
Therefore, the hypotenuse of the triangle or the length of the side of the shaded triangle is 17 inches.