We have the following function for the amount of carbon dioxide in moles produced in a chemical reaction:

And we also have that it is a function of time (t), and we need to find the rate of production of carbon dioxide after two seconds.
1. To find the rate of production, we need to find the derivative for the function since it will give us the instant rate of change for the chemical reaction. Then we have:
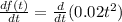
2. And now, applying the derivative rules for a constant, and for a power, we have:

3. Then after 2 seconds, we have that the rate of production of carbon dioxide is:
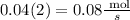
Therefore, in summary, the rate of production of carbon dioxide after two seconds is 0.08 mol/s (option c).