ANSWER
![\begin{equation*} \begin{cases}{g(x)=\sqrt[3]{x}}+1 \\ {} \\ {h(x)=4x^2-2}\end{cases} \end{equation*}](https://img.qammunity.org/2023/formulas/mathematics/high-school/5dozze0mzglh8dwm088c43o6of7826ym1q.png)
Step-by-step explanation
If f(x) is,
![f(x)=\sqrt[3]{4x^2-2}+1](https://img.qammunity.org/2023/formulas/mathematics/high-school/dyeyccdidchnrwfsb8jhhjidz693wv0vdx.png)
There are many possibilities for functions g(x) and h(x) such that f(x) = g(h(x)). One of them is that g(x) is,
![g(x)=\sqrt[3]{x}+1](https://img.qammunity.org/2023/formulas/mathematics/high-school/cs79ftd6salg71xvztyifnbejwgbwt116z.png)
And h(x) is,
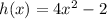
This way, in the composition g(h(x)), when we replace x in g(x) with h(x) we will get function f(x),
![g(h(x))=\sqrt[3]{h(x)}+1=\sqrt[3]{4x^2-2}+1](https://img.qammunity.org/2023/formulas/mathematics/high-school/2tu3zkyt67vnn5rt0wlvuqubhag9zt94ve.png)
Hence, one of the possible equations for g(x) and h(x) such that f(x) = g(h(x)) is:
![\begin{cases}{g(x)=\sqrt[3]{x}}+1 \\ {} \\ {h(x)=4x^2-2}\end{cases}](https://img.qammunity.org/2023/formulas/mathematics/high-school/dci2g4mwn2tosm6988wtzzvjv2wsvzsyaw.png)