Maximum value of a quadratic function
Given a quadratic function in the form:

The maximum or minimum value of the function occurs at the vertex of the parabola that represents the function.
The x-coordinate of the parabola is given by:
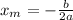
If a is positive, then the function has a minimum value, if a is negative, then the function has a maximum value.
The height of a ball h after t seconds is given by:
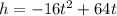
This is a quadratic function with a=-16, b=64, c=0
The time where the ball reaches its maximum height is:
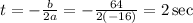
Now we substitute this value in the function:
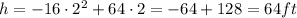
The maximum height of the ball is 64 ft