We have and equation for hearing loss:
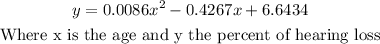
1. We want to know the percent of hearing loss at 18 years old, so we have to evaluate the equation at x=18:
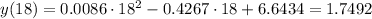
2. We want to find the percent range of hearing loss for the 30 - 60 years all. To do this we need to find the minimum and maximun of the equation at x between [30,60].
First we know the equation is a parabola, so we can find the minimun of the parabola, this is the vertex:
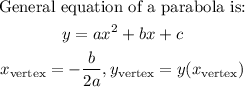
In this case, a=0.0086, b=-0.4267 and c=6.6434:
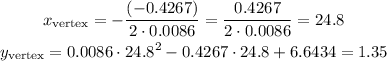
So, the minimun hearing loss is 1.35% at 24.8 years old, because 24.8 is not between 30 -60 years and it's less than 30, the minumun ot the range is in 30 years and the maximun at 60 years:

So, the range of hearing loss is [1.58, 12.0] at ages 30-60 years.
3. This is the same as point 2, we already has the value for 60 years, so we need to evaluate the equation at 84 years:
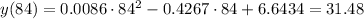
The range of hearing loss is [12.0, 31.48] ar ages 60-84 years.
4. Now we want to find the values of x where the y < 5, so:
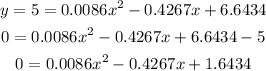
Now we need to find the roots with the formula:
![\begin{gathered} \text{General parabola form is:} \\ ax^2+bx+c \\ \text{and the roots are:} \\ x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4\cdot a\cdot c}}{2a} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gzymut3r1kuyjl1kwijrg0a27sdkc7240n.png)
In this case, a=0.0086, b=-0.4267 and c=1.6434
![\begin{gathered} x_(1,2)=\frac{0.4267\pm\sqrt[]{(-0.4267)^2-4\cdot0.0086\cdot1.6434}}{2\cdot0.0086} \\ x_(1,2)=(0.4267\pm0.3543)/(0.0172) \\ x_1=(0.4267+0.3543)/(0.0172)=45.4 \\ x_2=(0.4267-0.3543)/(0.0172)=4.2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/186ysf83n52x7gqucn7zycjpkzxtxgp1r1.png)
So, the people between 4.2 and 45.4 years has a hearing loss less than 5%.