Question

The denominator of a fraction is two more than three times the numerator. If both numerator and denominator are decreased by two, the simplified result is 2/7. Find the original fraction.

Answer 1

Let the numerator and denominator be x and y respectively

First statement: The denominator of a fraction is two more than three times the numerator

`y=\text{ 3x + 2}`

Second statement: . If both numerator and denominator are decreased by two, the simplified result is 2/7.

`(x-2)/(y-2)\text{ = }(2)/(7)`

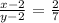
From the equations we have derived, we can now solve for x and y

From the second equation:

`\begin{gathered} (x-2)/(y-2)\text{ = }(2)/(7) \\ Cross-Multiply \\ 2(y-2)\text{ = 7\lparen x-2\rparen} \\ 2y\text{ - 4 = 7x - 14} \end{gathered}`

Substitute the expression for y from the first equation and solve for x:

`\begin{gathered} 2(3x\text{ + 2\rparen - 4= 7x -14} \\ 6x\text{ + 4 - 4 = 7x - 14} \\ Collect\text{ like terms} \\ 6x\text{ - 7x = -14} \\ -x\text{ = -14} \\ x\text{ = 14} \end{gathered}`

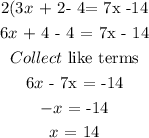
Substitute the value of x into the expression for y:

`\begin{gathered} y\text{ = 3x + 2} \\ y\text{ = 3\lparen14\rparen + 2} \\ y\text{ = 44} \end{gathered}`

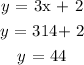
Hence, the original fraction was 14/44