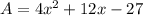We are given the following information.
Perimeter of rectangle = 8x + 12 units
Length of rectangle = 2x − 3 units
Recall that the perimeter of a rectangle is given by
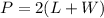
Where L is the length and W is the width of the rectangle.
Let us substitute the values of perimeter and length and solve for width.
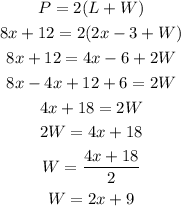
Recall that the area of a rectangle is given by
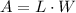
Substitute the values of length and width
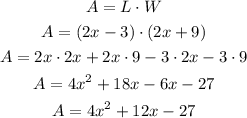
Therefore, the area of the rectangle is