Given the equation:
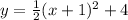
• You can identify that it has this form:
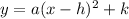
Where its Vertex is:
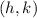
And the Focus is:
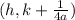
In this case, you can identify that:
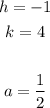
Therefore, you can determine that the Focus is:
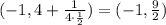
In order to write the y-coordinate of the Focus as a Mixed Numbers, you need to:
- Divide the numerator by the denominator.
- The Quotient will be the whole number part:
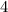
- The new numerator will be the Remainder:

- The denominator does not change.
Then:
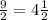
• In order to find the Directrix, you need to remember that, by definition, the Directrix has the same distance from the vertex that the Focus of the parabola is. Therefore:
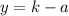
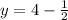
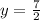
Apply the same procedure shown before, in order to convert the Improper Fraction to a Mixed Number. Hence, you get:
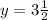
Therefore, the answer is: Option A.