Question

Where are the minimum and maximum values for f(x) = 2 sin x - 1 on the interval [0, 2π]?A. min:z = 0, 2 max:z =OB. min:z =max:z = 0,2플max:z = 0, 7, 2nC. min:z = max:z =D. min:z =Reset Selection

Answer 1

Recall that the maximum/minimum value of a function is the place where a function reaches its highest/lowest point.

We know that:

`\begin{gathered} For\text{ }all\text{ }x\in[0,2\pi] \\ -1\leq\sin(x)\leq1. \end{gathered}`

Multiplying the above result by 2 we get:

`\begin{gathered} -1*2\leq\sin(x)*2\leq1*2, \\ -2\leq2\sin(x)\leq2. \end{gathered}`

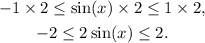
Subtracting 1 from the above inequality we get:

`\begin{gathered} -2-1\leq2\sin(x)-1\leq2-1, \\ -3\leq2\sin(x)-1\leq1. \end{gathered}`

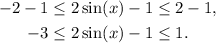
Therefore f(x) reaches a minimum at:

`x=(3\pi)/(2).`

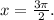
And f(x) reaches a maximum at:

`x=(\pi)/(2).`

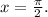
Answer: Option C.