Question

Find three consecutive intergers whose sum is 276

Answer 1

If we need to find three consecutive integers, we have that they can be written as follows:

`x,x+1,x+2`

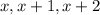
Since the sum of all of them is equal to 276, we can write the following equation:

`x+(x+1)+(x+2)=276`

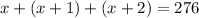
Now, adding like terms, we have:

`\begin{gathered} (x+x+x)+(1+2)=276 \\ 3x+3=276 \\ \end{gathered}`

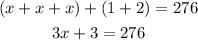
Now, we can subtract 3 from both sides of the equation, and then divide by 3 as follows:

`\begin{gathered} 3x+3-3=276-3 \\ 3x=273 \\ (3x)/(3)=(273)/(3) \\ x=91 \end{gathered}`

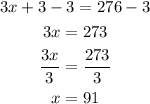
Then, we have that:

`\begin{gathered} x=91 \\ x+1=92 \\ x+2=93 \end{gathered}`

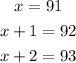
If we add these three consecutive integers, we will have:

`\begin{gathered} 91+92+93=276 \\ 276=276\Rightarrow This\text{ is True.} \end{gathered}`

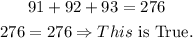
In summary, the three consecutive integers whose sum is 276 are 91, 92, and 93.