We need to find the values of "x" and "y" from two triangles that are congruent. If the triangles are congruent it means that the corresponding angles are equal. This means that angle R and angle N are the same, and from the angle sum theorem w know that the interior angles of triangle QPR sum 180, that is mathematically:
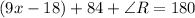
Since angle N is 3x+y, we replace that in the equation:
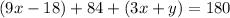
Simplifying we get:
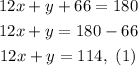
That gives us equation (1), but we need another equation since we have two variables. The other equation we get it from angles L and P, since this two angles must be equal. So we get the following equation:
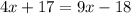
Solving for "x", we get:
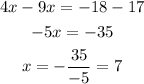
The value of "x" is 7. Now we input this value in equation (1), like this:
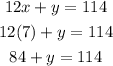
Solving for "y", we get:
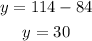
therefore, the value of "y" is 30.