Question

Use the compound interest formulas A=P(1+r/n)^nt and A=Pe^rt to solve. Find the accumulated value of $20,000 for 5 years at an interest rate of 6.5% if the money is compounded continuously . What is the accumulated value if the money is compounded continuously?

Answer 1

Given:

a.) Principal amount = $20,000

b.) Time = 5 years

c.) Interest Rate = 6.5%

To find the accumulated value if the money is compounded continuously, the following equation should be used:

`\text{ A = Pe}^{\text{rt}}`

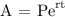
We get,

`\text{ A = \lparen20,000\rparen e}^{((6.5)/(100))(5)}`
`\text{ A = \lparen20,000\rparen}^\text{e}^((0.065)(5))`
`\text{ A = \$27,680.61291961503 }\approx\text{ \$27,680.61}`

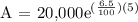
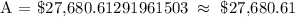
Therefore, the accumulated amount when compounded continuously is approximately $27,680.61