Answer:
Step-by-step explanation:
Given the below inequality;
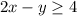
The slope-intercept form of the equation of a line is generally given as;

where m = slope of the line
b = y-intercept of the line
Let's go ahead and rewrite the given inequality in slope-intercept form by subtracting 2x from both sides, multiplying both sides by -1, and reversing the inequality sign;

If we compare the slope-intercept equation with the above inequality, we can see that the graph of the inequality will have a slope(m) of 2 and a y-intercept(b) of -4.
Since the inequality has both an inequality sign and an equality sign, the line will be a solid line.
Since the inequality has a less than sign, we'll shade the region below the line.
See below the graph of the given inequality with the shaded region;