Question

In the triangle shown we can find the angle as follows.A153936(a) = sin-X(b) 0 - cos(C) 0 = tan-10

Answer 1

We need to calculate the three trigonometrics relations on the right triangle. They are as follow:

`\begin{gathered} \sin \theta=(36)/(39)=0.92 \\ \cos \theta=(15)/(39)=0.38 \\ \tan \theta=(36)/(15)=2.4 \end{gathered}`

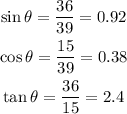
We need to use this values on each option. The "sin^-1" is the inverse of the sine, the "cos^-1" is the inverse of the cosine and the "tan^-1" is the inverse of the tangent. If we use these values on the functions we will find the value of theta.

`\sin ^(-1)0.92=\text{ 66.93}`

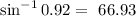
The angle is equal to 66.93 degrees