Question

Please help me solve question 5 on my algebra homework

Answer 1

Check the answers below, please

1) Since we have this linear function:

`f(x)=-(1)/(3)x-4`

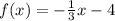
a) We can proceed to state the Domain, the set of inputs for this function as:

`D=(-\infty,\infty)`

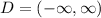
Since this Linear function does not have any restraint or discontinuity.

b) The Range, i.e. the set of outputs for this function will be defined for this function as:

`R=(-\infty,\infty)`

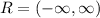
c) The Zero, can be found algebraically by plugging f(x)=0

`\begin{gathered} f(x)=-(1)/(3)x-4 \\ 0=-(1)/(3)x-4 \\ (1)/(3)x=-4 \\ x=-12 \end{gathered}`

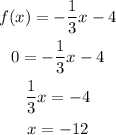
d) Y-intercept is the point in the y-axis where the line intercepts it. Looking at the rule of the function, we can state the y-intercept as:

`-4`

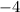
e) Slope, the measure of how steep a line of a function is, it's always the coefficient of x, in this case:

`m=-(1)/(3)`

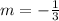
f) Type of slope. Since the slope is -1/3 , i.e. lesser than 0, then we can classify it as decreasing

g) Evaluating f(3):

`\begin{gathered} f(x)=-(1)/(3)x-4 \\ f(3)=-(1)/(3)(3)-4 \\ f(3)=-1-4 \\ f(3)=-5 \end{gathered}`

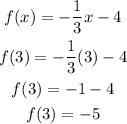
h) The value of x, where f(x)= -4 Similarly to the previous item, we can plug into that f(x)= -4 like this:

`\begin{gathered} f(x)=-(1)/(3)x-4 \\ -4=-(1)/(3)x-4 \\ -4+4=-(1)/(3)x-4+4 \\ -(1)/(3)x=0 \\ \mathbf{x=0} \end{gathered}`

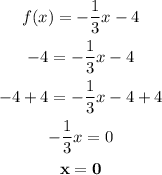
i) The graph can be traced having the zero, the y-intercept the type of the slope we can plot this: