48 minutes
1) We can solve this problem using a Linear System of Equations. Let's call walk "w" and bike by "b
2)So we can set the following system, considering the given data:
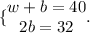
Thus, let's solve it by the Substitution Method. Let's solve the II equation for b:
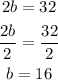
2.2)We can plug that into the first equation and then find how long did it take to go walking to school:
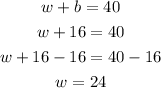
Notice that the question wants to know how long does it take to go to school walking home to school and back, so we can write out:
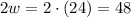
3) Hence, Ben would take 48 minutes to go walking home to school and back