Question

Gave a nuclear physicist needs 50 liters of a 60 percent acid solution. He currently has a 20% solution and a 70% solution. How many liters of each does he need to make the needed 50 liters of 60% acid solution?

Answer 1

Let the number of liters of 20% solution be "x"

Let the number of liters of 70% solution be "y"

According to the problem, we need 50 liters of the solution. Thus, we can write >>>>

`x+y=50`

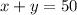
Also, given, we need 50 L of 60% solution. Thus, we can write >>>>>

`0.2x+0.7y=0.6*50`

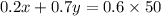
Let's substitute first equation into the second and solve for "x" >>>>>

`\begin{gathered} x+y=50 \\ 0.2x+0.7y=0.6*50 \\ --------------- \\ y=50-x \\ \text{Substituting,} \\ 0.2x+0.7(50-x)=30 \\ 0.2x+35-0.7x=30 \\ 0.5x=5 \\ x=(5)/(0.5) \\ x=10 \end{gathered}`

So, the "y" value is >>>

`\begin{gathered} x+y=50 \\ 10+y=50 \\ y=50-10 \\ y=40 \end{gathered}`

So, he needs,

Answer

10 liters of 20% solution

40 liters of 70% solution