The problem says "3 1/2 cups of sugar took one cup of chocolate chips"
The ratio is: 3 1/2 sugar for each cup of chocolate.
We want to find the quantity of chocolate chips for "one and three-quarter cups of sugar"
First, let's convert 3 1/2 into an improper fraction:
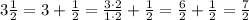
Now, we want to find an expression for "one and three-quarter". We can write:
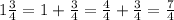
And now, we can use cross multiplication. If 7/2 of sugar needs 1 cup of chocolate, how many of chocolate if 7/4 of sugar is used? If we call x to the quantity of chocolate needed, we can wirte:
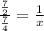
Now take the reciprocal on both sides:

And solve:
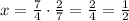
Thus, the answer is: According to the recipe, the quantity of chocolate needed is 1/2 cup.