Question

A student drops a feather from a height of 89.0m. Determine all unknowns and answer the following questions.How long did the feather remain in the air? What was the feather's speed just before striking the ground?

Answer 1

The vertical distance covered by the feather is,

`h=ut+(1)/(2)gt^2`

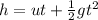
As the feather is falling freely therefore, the initial speed of the feather is zero.

Substitute the known values and solve to calculate the time taken.

`\begin{gathered} 89.0\text{ m=(0 m/s)t+}(1)/(2)(9.8m/s^2)t^2 \\ t^2=\frac{2(89.0\text{ m)}}{(9.8m/s^2)} \\ t=\sqrt[]{18.16s^2} \\ \approx4.26\text{ s} \end{gathered}`

Therefore, the time for which the feather remain in the air is 4.26 s.

The final speed of the feather can be given as,

`v=u+gt`

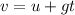
Substitute the known values,

`\begin{gathered} v=0m/s+(9.8m/s^2)(4.26\text{ s)} \\ \approx41.75\text{ m/s} \end{gathered}`

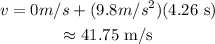
Therefore, the speed with which it strikes on the ground is 41.75 m/s.