Answer:
The speed of the jet is 150 mph
Step-by-step explanation:
Let x represent the speed the jet.
The speed of the wind is 25 mph
Let t represent the time
Given that the jet can fly 1210 miles against the headwind, then

It can fly 1694 miles against the tailwind, then

From (1) and (2)
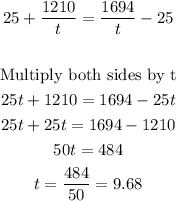
With t = 9.68 hours, we can find x by sustituting the value into either of (1) or (2)
Using (2)
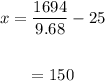
The speed of the jet is 150 mph