Question

I don’t understand this at all. Could you break it down for me?

Answer 1

#6

Vertical angles are the angles opposite each other when two lines cross.

Let's see which angle forms a "X" with ∠EOD:

So, ∠COF is "vertical" with ∠EOD.

═══════════════════════════════════════════════

#7

When 2 angles add up to 90 degrees, we say that they are complementary angles.

Since ∠POF + ∠FOB = 90, then ∠POF is complementary to ∠FOB.

═══════════════════════════════════════════════

#8

∠BOC + ∠AOC is a straight angle (straight line).

A straight angle is 180 degrees.

So, we can write,

`\angle BOC+\angle AOC=180\degree`

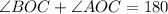
We know ∠BOC = 150, so ∠AOC will be,

`\begin{gathered} 150\degree+\angle AOC=180\degree \\ \angle\text{AOC}=180-150 \\ \angle\text{AOC}=30\degree \end{gathered}`

═══════════════════════════════════════════════

#9

From the diagram, we can see that ∠EOA and ∠FOB are vertical angles. Thus, they are equal.

Since ∠EOA = 37,

∠FOB = 37

Now, from the diagram, we can see,

∠FOA + ∠FOB = 180 [since they are straight line]

Now, we can easily find ∠FOA:

`\begin{gathered} \angle FOA+\angle FOB=180 \\ \angle\text{FOA}+37=180 \\ \angle\text{FOA}=180-37 \\ \angle\text{FOA}=143\degree \end{gathered}`

═══════════════════════════════════════════════

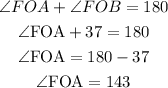
#10

Adjacent angles are two angles that have a common side and a common vertex (corner point) but do not overlap in any way.

For example,

∠1 and ∠2 are adjacent angles.

From our diagram,

∠HGO is adjacent to ∠EGH

From the diagram above, we see that G is the common vertex and GH is the common side.

Thus,

∠HGO is adjacent to ∠EGH

═══════════════════════════════════════════════

#11

From the diagram, we see that ∠EGH and ∠HGO fall in a straight line. So, they add up to 180 degrees.

`\angle\text{EGH}+\angle\text{HGO}=180`

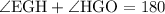
Given,

∠HGO = 128,

Let's find ∠EGH:

`\begin{gathered} \angle\text{EGH}+\angle\text{HGO}=180 \\ \angle\text{EGH}+128=180 \\ \angle\text{EGH}=180-128 \\ \angle\text{EGH}=52\degree \end{gathered}`

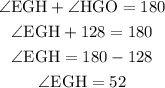
Given,

`\angle\text{EGH}\cong\angle\text{DOB}`

We can say:

`\angle\text{DOB}=52\degree`

═══════════════════════════════════════════════

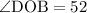
#12

From the figure, we see that ∠EOA + ∠EOD + ∠DOB = 180 degrees [straight line].

Given,

∠EOA = 67

∠DOB = 29

We can solve for ∠EOD:

`\begin{gathered} \angle EOA+\angle EOD+\angle DOB=180 \\ 67+\angle\text{EOD}+29=180 \\ 96+\angle\text{EOD}=180 \\ \angle\text{EOD}=180-96 \\ \angle\text{EOD}=84\degree \end{gathered}`

═══════════════════════════════════════════════

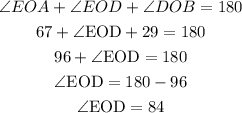
#13

When 2 angles add up to 180 degrees, we say that they are supplementary angles.

Given,

∠AOD + ∠DOB = 180

We can say that ∠AOD is supplementary to ∠DOB.

═══════════════════════════════════════════════

#14

Since ∠COF is congruent to ∠DOF and fall is a straight line, we can say that they are each 90 degrees.

Thus, FO and CD will be perpendicular to each other.

So, we can say,

FO is perpendicular to CD

═══════════════════════════════════════════════

#15

Given,

∠COP = 72 and ∠POF = 31, we have:

We want to know the measure of ∠EOD.

Let's see below:

We see that ∠COF and ∠EOD are vertical angles.

Vertical angles are equal.

So,

∠EOD = ∠COP + ∠POF

∠EOD = 72 + 31

∠EOD = 103°

'~'-.,__,.-'~'-.,__,.-'~'-.,__,.-'~'-.,__,.-'~'-.,__,.-'~'-.,__,.-'~'-.,__,.-'~'-.,__,.-'~'-.,__,.-

Answers
`\begin{gathered} 6.\angle\text{COF} \\ 7.\text{Complementary} \\ 8.\angle\text{AOC}=30\degree \\ 9.\angle\text{FOA}=143\degree \\ 10.\angle\text{HGO} \\ 11.\angle\text{DOB}=52\degree \\ 12.\angle\text{EOD}=84\degree \\ 13.Supplementary \\ 14.Perpendicular \\ 15.\angle\text{EOD}=103\degree \end{gathered}`