Answer:
2 pounds of apples and 6 pounds of bananas or 4 pounds of apples and 2 pounds of bananas. 2a + b ≤ 10
Step-by-step explanation:
We were given that:
Tony has $10 to buy apples and bananas for a fruit salad
Apples cost $2 per pound and bananas cost $1 per pound
Let apples be represented by "a" & bananas with "b"
We will use the information above to generate the inequality below:
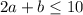
For 2 pounds of apples and 13 pounds of bananas or 4 pounds of apples and 18 pounds of bananas, we have:
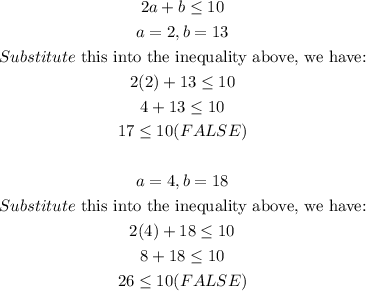
For 2 pounds of apples and 6 pounds of bananas or 4 pounds of apples and 2 pounds of bananas, we have:
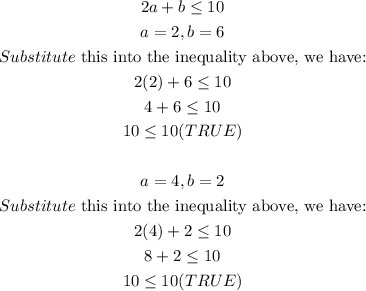
Therefore, the correct option is:
2 pounds of apples and 6 pounds of bananas or 4 pounds of apples and 2 pounds of bananas. 2a + b ≤ 10