Question

A triangular field has sides of 120.32 m and 204.61 m, and the angle between them measures 60.881°. Find the area of the field.A. 14,015.0 m²B. 11,810.7 m²C. 10,753.5 m²D. 11,333.6 m²

Answer 1

Let's draw the scenario to better understand the problem:

For us to be able to determine the area of the field, we will be using the following formula:

`\text{ Area = }ab\text{ }\frac{\text{ sin }\theta}{2}`

Where,

a = 120.32 m

b = 204.61 m

θ = the angle between the two sides or the included angle = 60.881°

We get.

`\text{ Area = }ab\text{ }\frac{\text{ sin }\theta}{2}`
`\text{ = }\frac{\text{(120.32)(204.61)(Sin 60.881}^(\circ))}{\text{ 2}}`
`\text{ = }\frac{\text{(}24,618.6752\text{)(Sin 60.881}^(\circ))}{\text{ 2}}`
`\text{ = }(12,309.3376)(Sin60.881^(\circ))`
`\text{ Area = 10,753.5715 }\approx\text{ 10,753.5 sq. m.}`

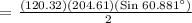
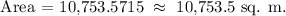
Therefore, the area of the field is 10,753.5 sq. m.

The answer is letter C