If we have the system:

and we don't want the system to have a solution we need that one equation contradicts the other. For example if we choose a=3, b=1 and c=3, we have the system:
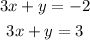
notice that the left side on both equations is the same, whereas the right side is not the same; this means that the second equation contradicts the first one, hence the system does not have a solution.
This form of choosing a, b and c can be extend to and infinite number of systems if we only change the value of c, that is, as long as a=3, b=1 and that c is not -2 the sytem will not have a solution.