Question

Write an equation of a line in slope-intercept form that is perpendicular to the line to y = -2x - 1 and that passes through the point (-10,4)

Answer 1

Answer:
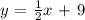
`y\text{ = }(1)/(2)x\text{ + 9}`Explanations:

The slope - Intercept form of the equation of a line is written as:

y = mx + c...........................(1)

where m is the slope and

c is the intercept

the equation given in this task is:

y = -2x - 1..........................(2)

Comparing equations (1) and (2)

m = -2

That is the slope of the line = -2

A line perpendicular to the line y = -2x - 1 will have a slope:

`\begin{gathered} m_1=\text{ }(-1)/(m) \\ m_1=\text{ }(-1)/(-2) \\ m_1=\text{ }(1)/(2) \end{gathered}`

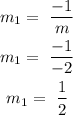
The equation of the perpendicular line will be:

`y-y_1=m_1(x-x_1)`

The point through which the line passes is (-10, 4)

That is, x₁ = -10, y₁ = 4

The equation of the perpendicular line becomes:

`\begin{gathered} y\text{ - 4 = }(1)/(2)(x\text{ - (-10))} \\ y\text{ - 4 = }(1)/(2)(x\text{ + 10)} \\ y-\text{ 4 = }(x)/(2)+\text{ }(10)/(2) \\ y\text{ - 4 = }(x)/(2)\text{ + 5} \\ y\text{ = }(x)/(2)\text{ + 5 + 4} \\ y\text{ = }(x)/(2)\text{ + 9} \\ y\text{ = }(1)/(2)x\text{ + 9} \end{gathered}`